1. 关于算法的时间/空间复杂度
| Big-O | 名称 | 描述 |
|---|---|---|
| O(1) | 恒定(Constant) | 最好,程序执行的结果与输入数据量大小无关,总是需要相同的时间/空间量,例如:用索引查找数组元素。 |
| O(logN) | 对数(Constant) | 非常好,时间或空间性能与输入呈对数比例增长。即使对于大量的数据,这也是非常快的。例子:二进制搜索。 |
| O(n) | 线性(Linear) | 良好,时间或空间性能与输入呈对数比例增长。例子:顺序搜索。 |
| O(NlogN) | 线性化(Linearithmic) | 不错,比线性略差,但也不坏。 |
| O(N^2)) | 平方(Quadratic) | 较慢,时间或空间性能与输入呈平方比例增长。通常使用两层嵌套循环的算法都属于此类,如:插入排序、冒泡排序。 |
| O(N^3) | 立方(Cubic) | 不佳,时间或空间性能与输入呈平方比例增长。如:矩阵乘法。 |
| O(2^N) | 指数级(Exponential) | 非常差,输入的少量增加即可使得运行事件加倍。如:旅行推销员问题。 |
| O(N!) | 阶乘(Factorial) | 不能忍受,做任何事情都需要一百万年的时间。 |
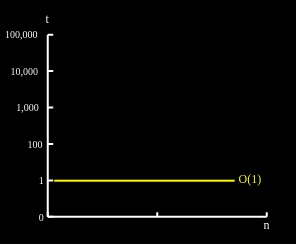
1.1 O(1) - 固定时间/空间(Constant)
O(1)表示无论输入的大小怎样,一个算法都将在相同的时间或空间内完成。
1 | int n = 1000; |
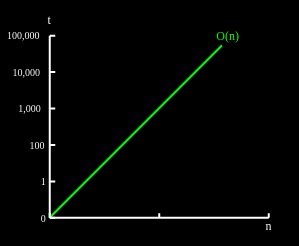
1.2 O(n) - 线性
O(1)表示一个算法的时间或空间与输入呈线性比例增长。
1 | for (int i =0; i < n; i++) { |
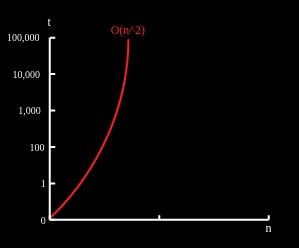
1.3 O(n^2) - 平方
O(n^2)表示一个算法的时间或空间性能与输入呈平方比例增长。
1 | for (int i = 0; i < n; i++) { |
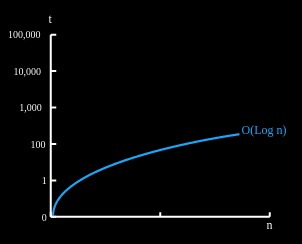
1.4 O(log n) - 对数
O(log n) 表示一个算法的时间或空间性能与输入呈对数比例增长。
1 | for (int i = 0; i < n; i *= 2) { |
1.5 O(NlogN) 线性化(linearithmic)
线性化算法对于非常大的数据量来说但是比较好的,比如快速排序、归并排序、堆排序等。
1 | for (int i = 0; i < n; i++ ) |
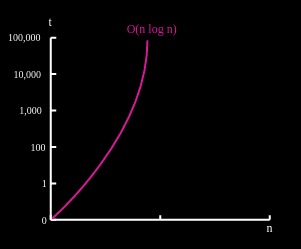
总结:
算法的复杂度分析可以帮助你理解一个算法的事件或者空间性能,上面各种复杂度放在一起比较可以有一个直观的认识:
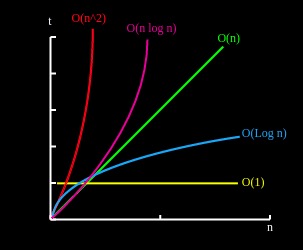
2. 排序算法

2.1 冒泡排序
依次比较相邻的两个数,较小数放前面,较大数放后面,直到最大数放在最后, 然后重复操作,最后排序为升序。
演示:

第一层循环为重复的次数,循环次数为array.length-1
第二次循环为依次比较相邻的数,循环次数为array.length-1-i
1 | for (int i = 0; i < arr.length - 1; i++){ |
2.2 选择排序
选择排序是一种简单直观的排序算法,无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
- 算法步骤
- 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
- 再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
- 重复第二步,直到所有元素均排序完毕。
- 动图演示
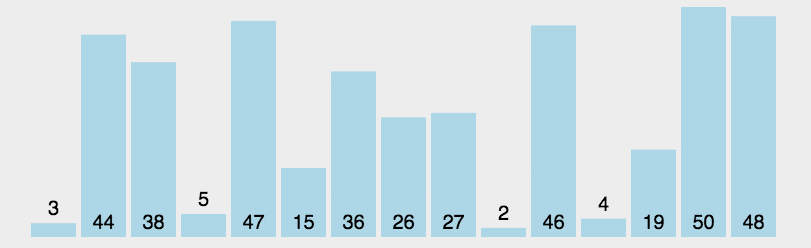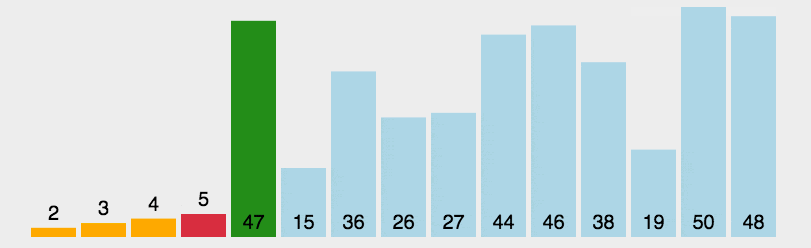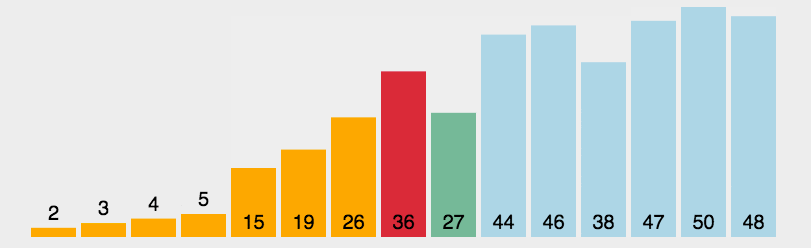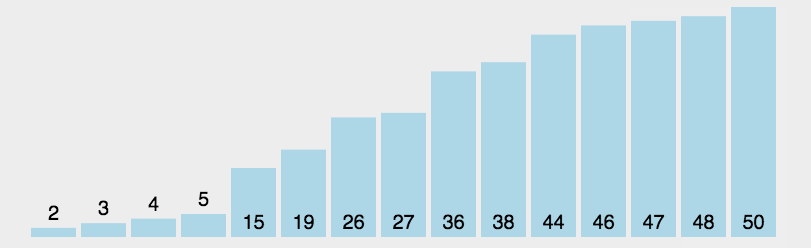
1 | public void sort(int[] arr) { |
2.3 插入排序
插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴,但它的原理应该是最容易理解的了,
插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
演示: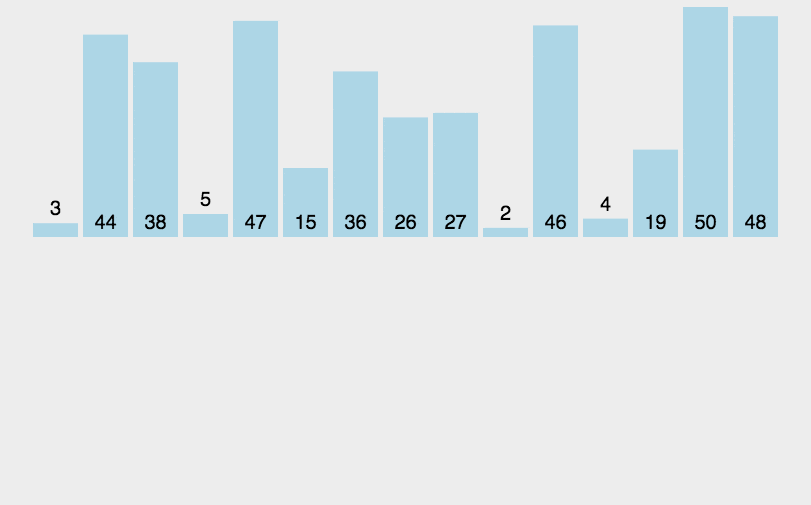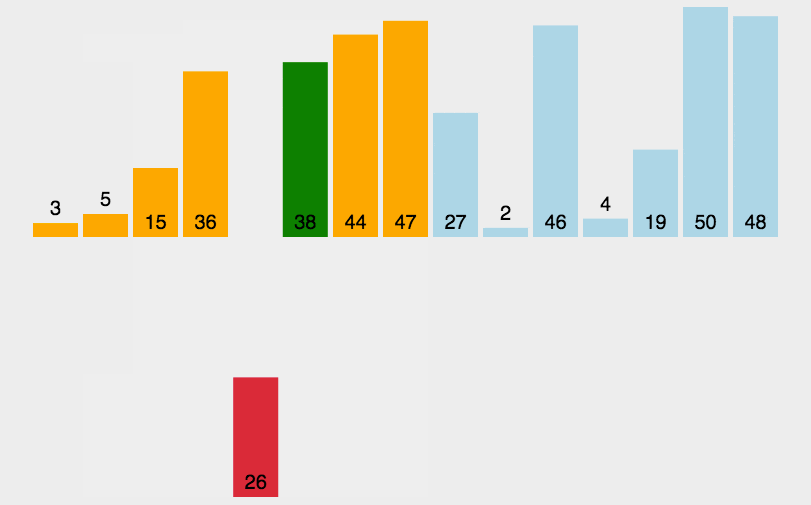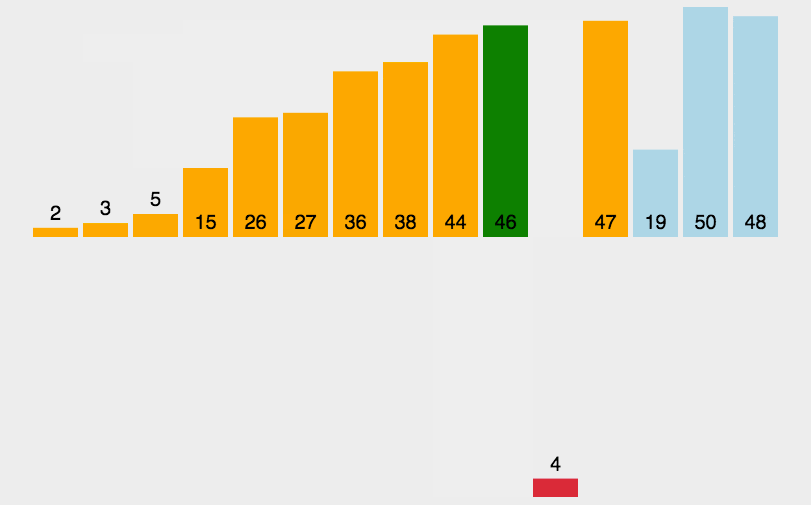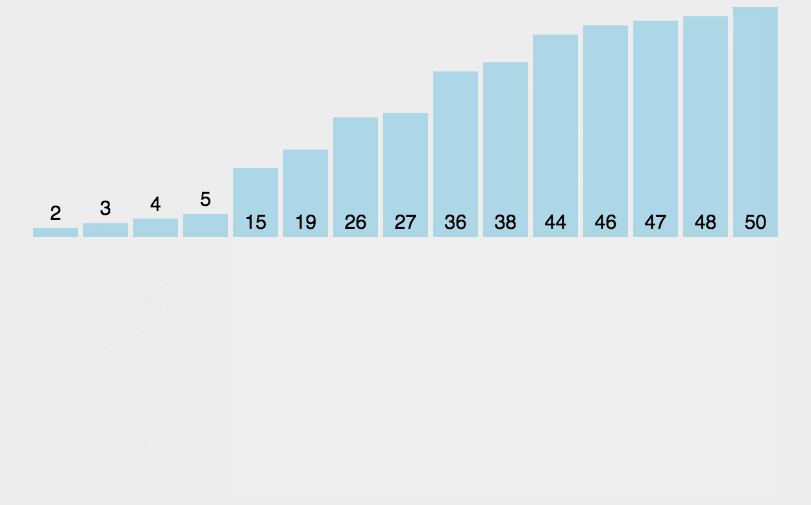
1 | public void sort(int[] arr) { |
[6, 1, 2, 7, 9, 3, 4, 5, 10, 8]
- 第一轮:
1 | i = 1 |
- 第二轮
1 | i = 2; |
2.4 希尔排序
通过增量(gap)将元素两两分组,对每组使用直接插入排序算法排序;增量(gap)逐渐减少,当增量(gap)减至1时,整个数据恰被分成一组,最后进行一次插入排序,整个数组就有序了。
演示:
第一轮:

第二轮:
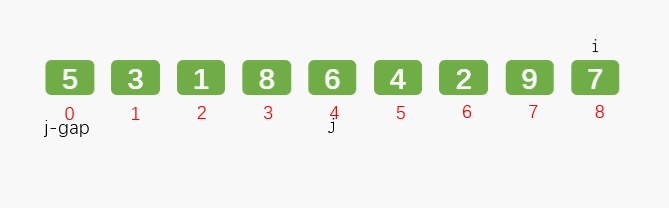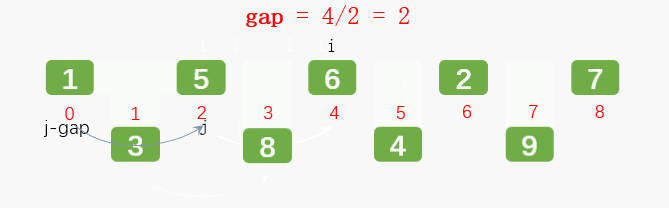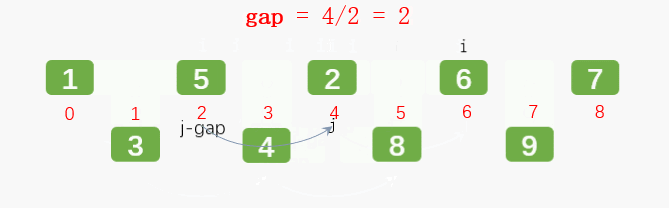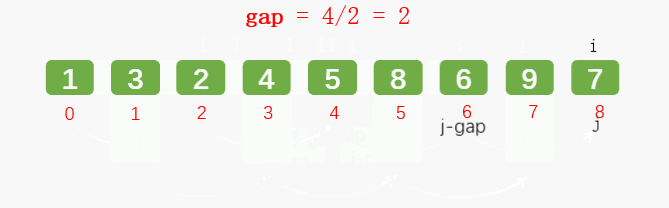
第三轮:

参考https://zhuanlan.zhihu.com/p/122472667
代码:
1 | public void sort(int[] arr) { |
2.5 归并排序
演示: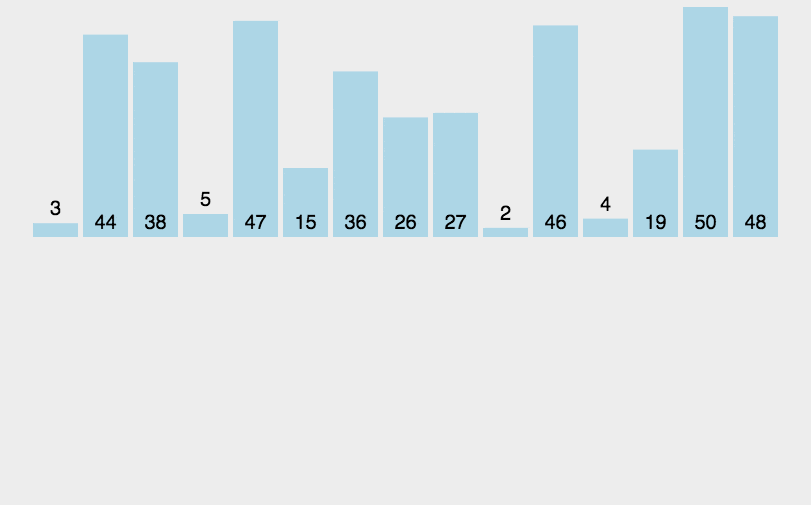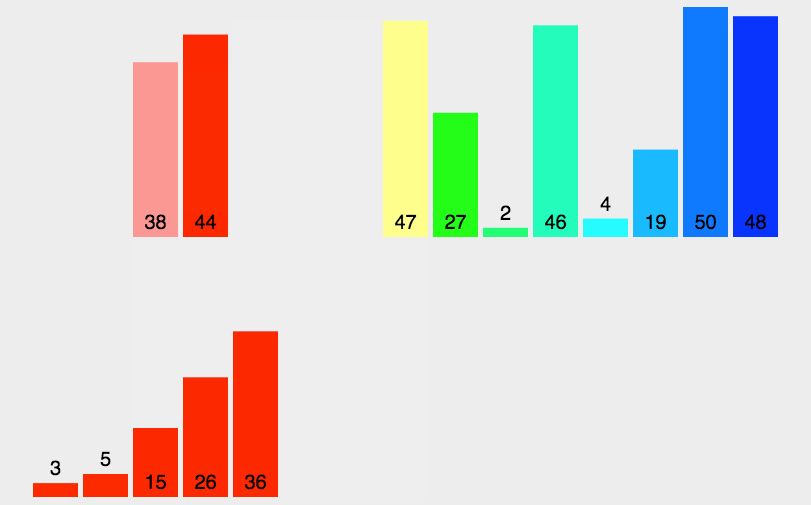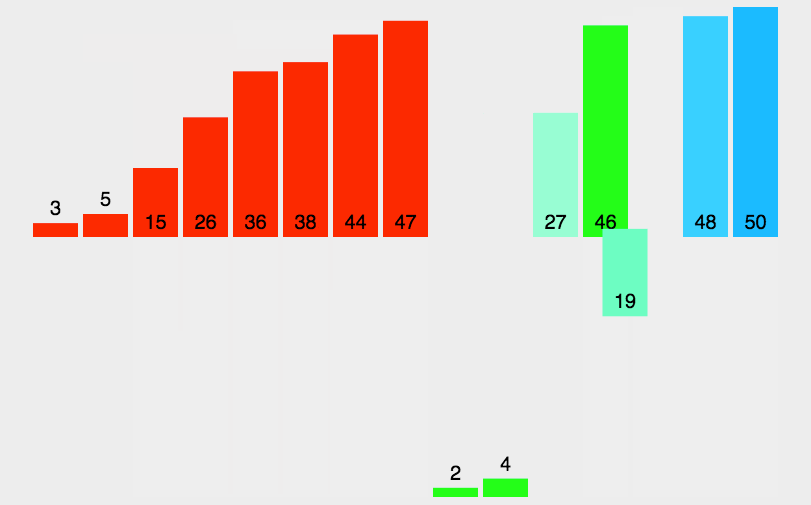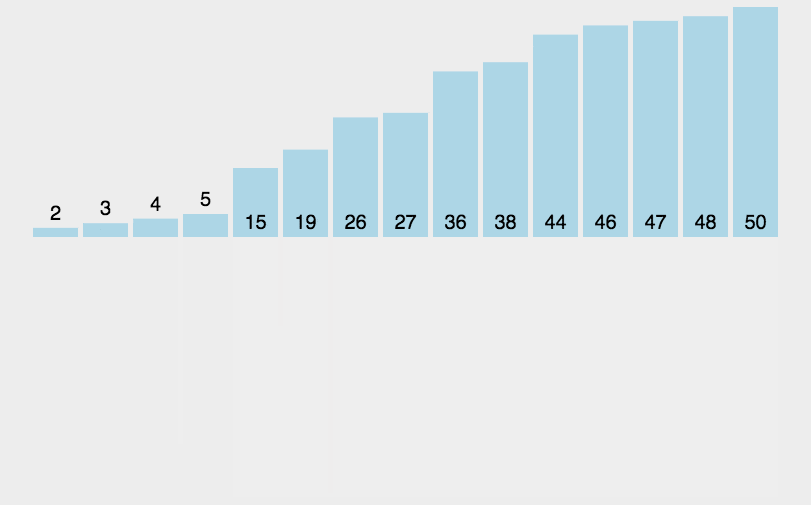
2.6 快速排序
算法思想:选择序列中一个元素作为基准元素base,维护两个指针front和back分别指向序列的首尾,
首先用front指向的元素和base进行比较,如果大于base,则与back指向的元素进行交换,否则指针右移;
然后比较back指向的元素是否小于base,返回为true则与front指向的元素进行交换,否则指针左移。
前后交替这样就能保证较小数都放在base的左边,较大数在base的右边,然后递归调用对各部分继续排序,直到最后排好序。
1 | public void sort(int[] sourceArray) { |
1 | [6, 1, 2, 7, 9, 3, 4, 5, 10, 8] |
- 第一轮:
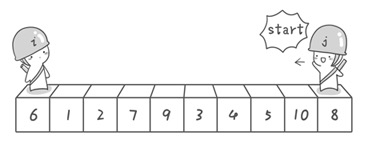
1 | 基准为6:左边找个大的,右边找个小的: |
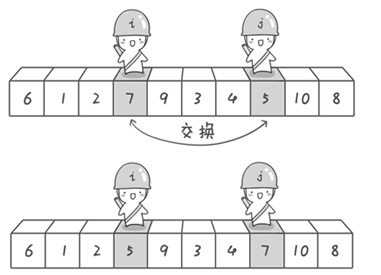
1 | 继续左边找个大的,右边找个小的: |
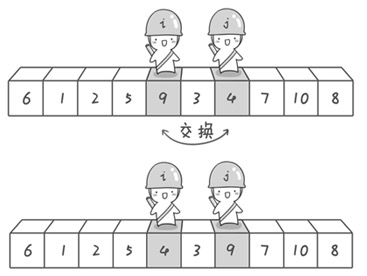
1 | 交换pivot和patation index |

然后两边再次递归使用快速排序,知道每个patation都只有一个元素为止。
- 第二轮(左边):
1 | [3, 1, 2, 5, 4] |
- 第三轮(左边):
1 | [2, 1] |
- 第四轮(左边):
1 | [5, 4] |
至此,第一轮左边patition部分均已排序完成
- 第五轮(右边):
1 | [9, 7, 10, 8] |
- 第六轮(右边):
1 | [8, 7] |
至此,数组排序完成:
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
2.7 堆排序
演示:
2.8 计数排序
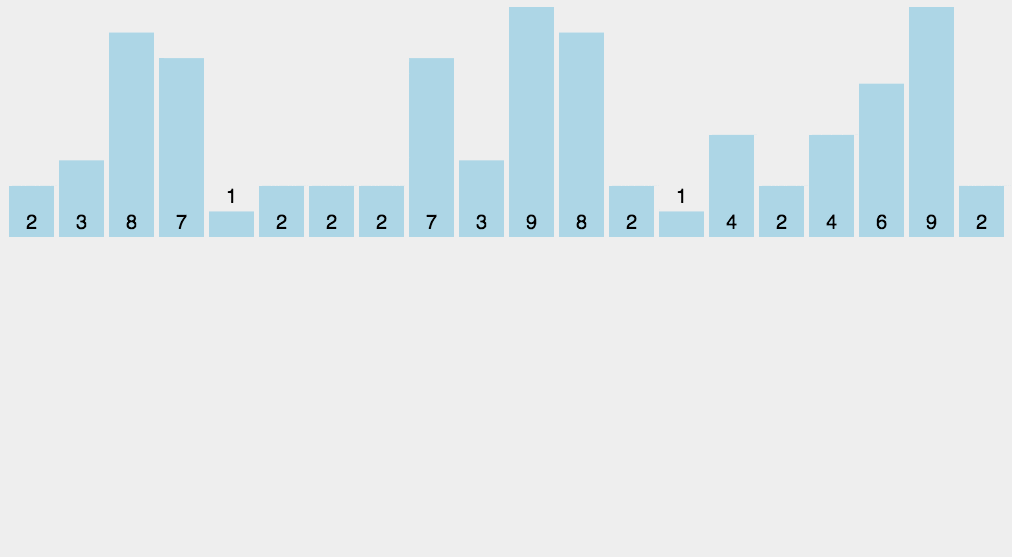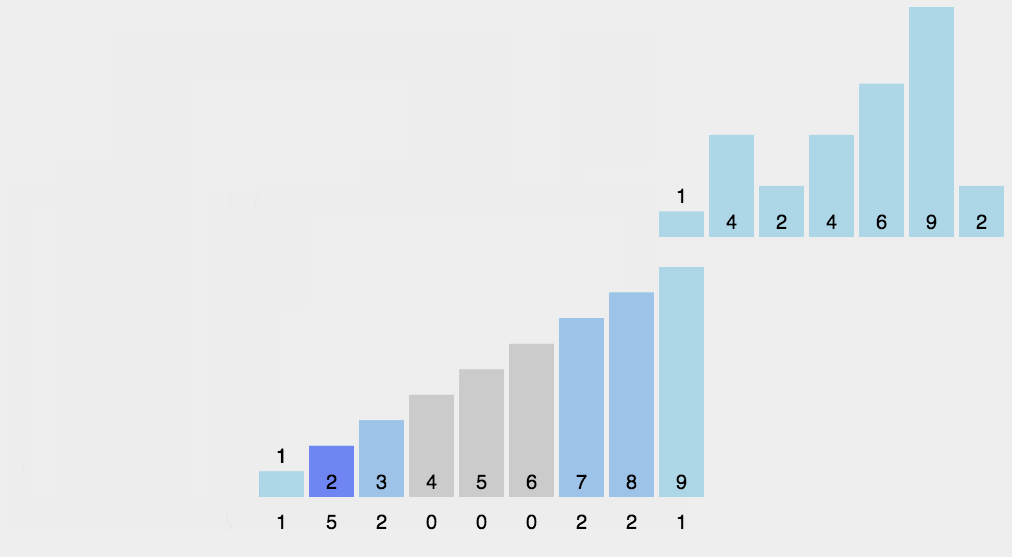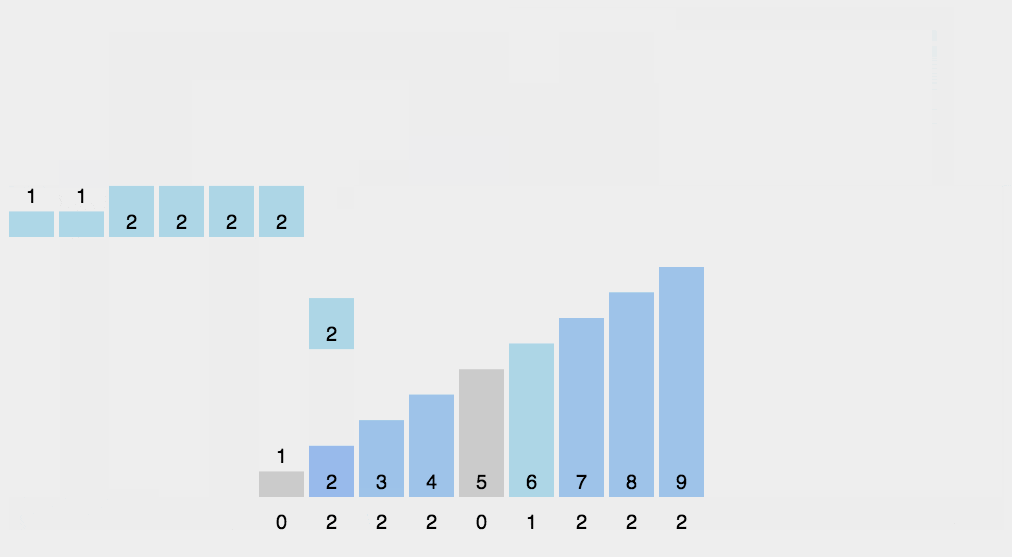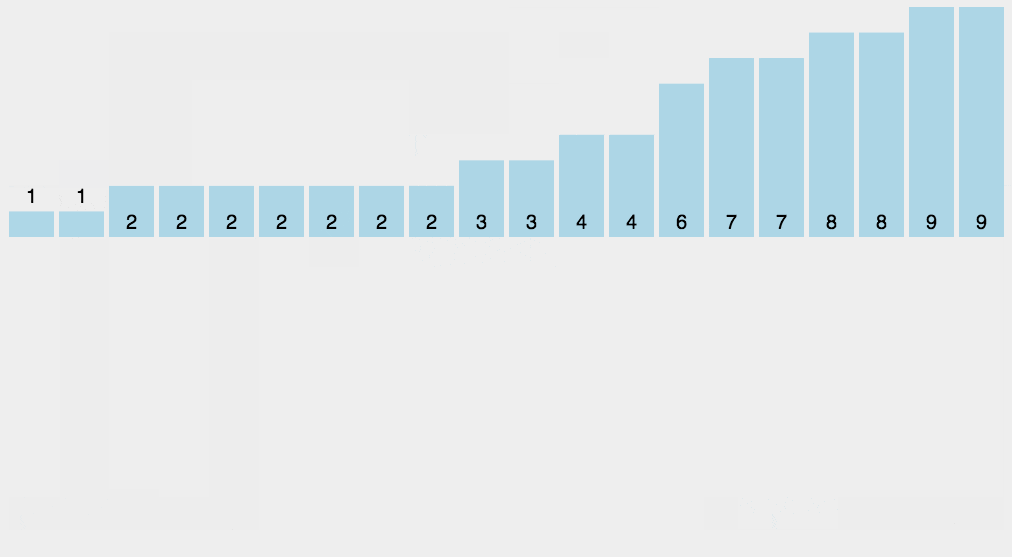
2.9 桶排序

2.10 基数排序
